Worked example: estimating a single proportion

Packages

library(tidyverse)
library(tidymodels)

Data

In a survey conducted by Survey USA between September 30, 2023 and October 3, 2023, 2759 registered voters from all 50 US states were asked

America will hold an election for President of the United States next November. Not everyone makes the time to vote in every election. Which best describes you? Are you certain to vote? Will you probably vote? Are the chances you will vote about 50/50? Or will you probably not vote?

The data from this survey can be found in voting-survey.csv:

voting_survey <- read_csv("voting-survey.csv")

Rows: 2759 Columns: 2
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): vote
dbl (1): id

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(voting_survey)

Rows: 2,759
Columns: 2
$ id   <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19…
$ vote <chr> "Certain to vote", "Certain to vote", "Certain to vote", "Certain…

Visualize and summarize the data

This simple bar plot displays the number of respondents who gave each of the five possible answers:

ggplot(voting_survey, aes(y = vote)) + 
  geom_bar()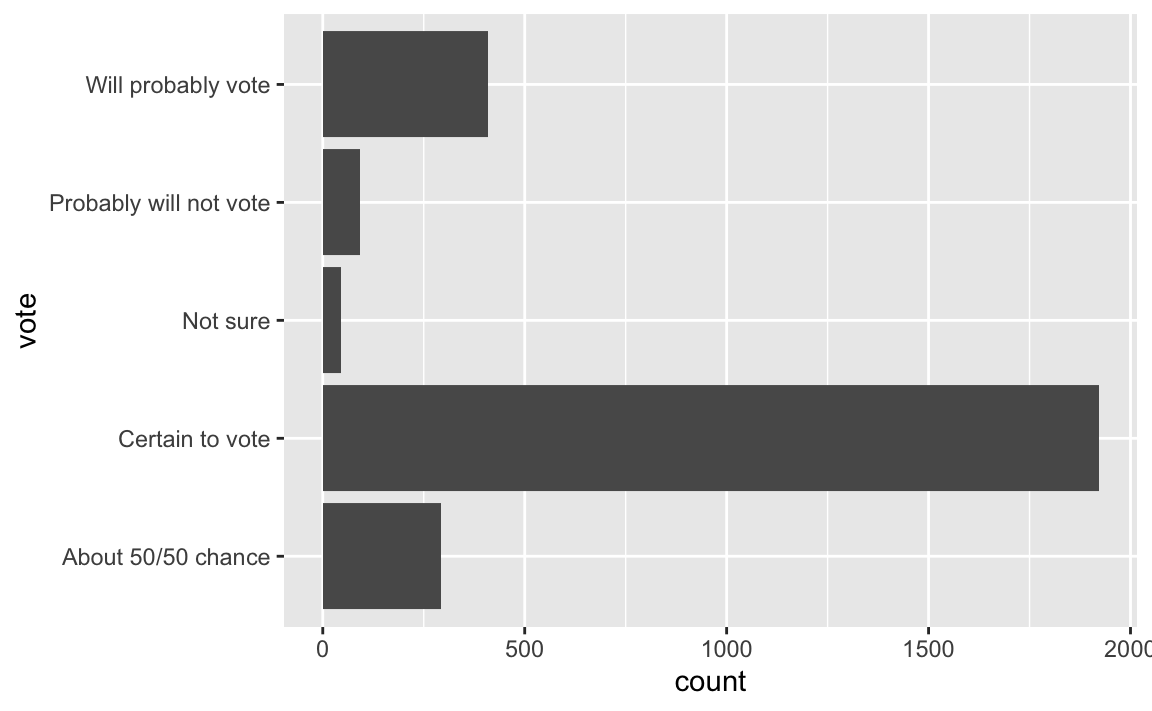

This code calculates the proportion of respondents that gave each answer:

voting_survey |>
  count(vote) |>
  mutate(props = n / sum(n))

# A tibble: 5 × 3
  vote                       n  props
  <chr>                  <int>  <dbl>
1 About 50/50 chance       293 0.106 
2 Certain to vote         1921 0.696 
3 Not sure                  44 0.0159
4 Probably will not vote    92 0.0333
5 Will probably vote       409 0.148 

Interval estimation

Based on these data, we want to estimate the true proportion of registered US voters who are certain to vote in the next presidential election. Our point estimate based on the survey responses is 69.6%, but how reliably estimated is that? To answer this, we need to construct a confidence interval.

# Prepare the data for analysis (pre-processing)

voting_survey <- voting_survey |>
  mutate(vote = if_else(vote == "Certain to vote", "Certain to vote", "Not certain to vote"))

set.seed(20)

boot_dist <- voting_survey |>
  specify(response = vote, success = "Certain to vote") |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "prop")

ci <- boot_dist |>
  get_ci()
ci

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1    0.679    0.714

visualize(boot_dist) + 
  shade_ci(ci)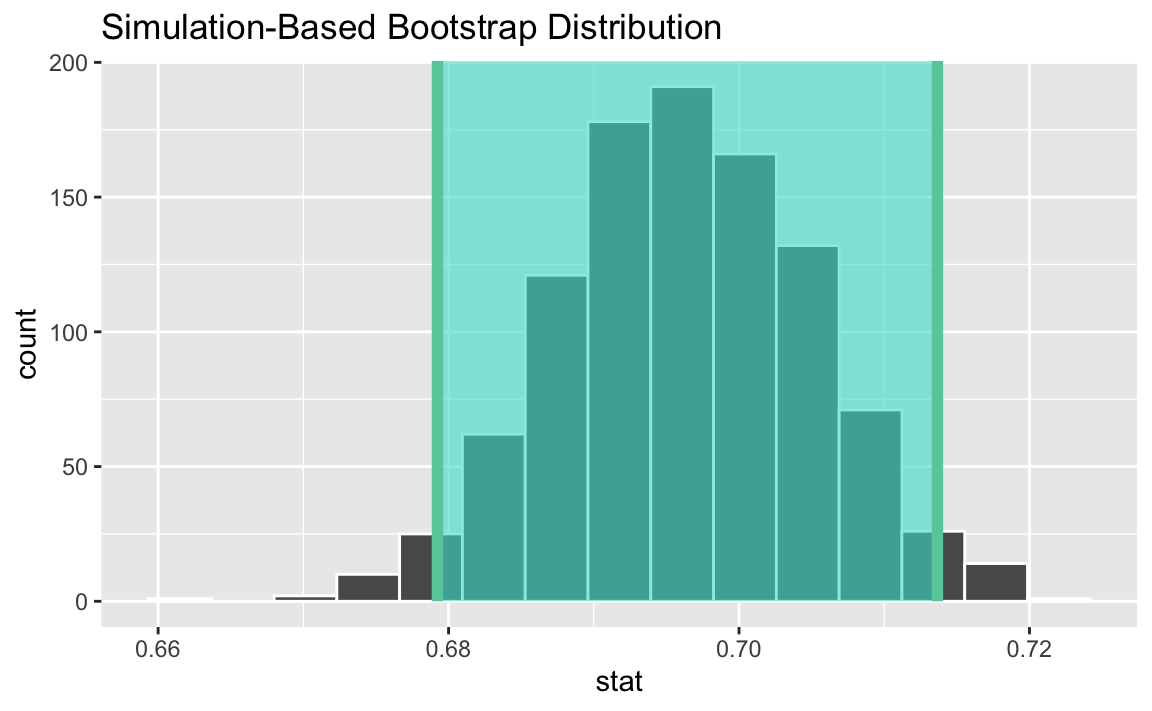

Hypothesis testing

Pew says that 66% of eligible US voters turned out for the 2020 presidential election. A newspaper claims that even more people will turnout in 2024, and cites this survey as evidence. Do these data provide convincing evidence for this claim?

The formal hypotheses are

\[ \begin{aligned} \text{H}_0: p&=0.66\\ \text{H}_A: p&>0.66, \end{aligned} \] where \(p\) is the true proportion that say they are guaranteed to turn out in 2024.

# compute the observed proportion

obs_stat <- voting_survey |>
    specify(response = vote, success = "Certain to vote") |>
    calculate(stat = "prop")

# simulate the null distribution

set.seed(525600)

null_dist <- voting_survey |>
  specify(response = vote, success = "Certain to vote") |>
  hypothesize(null = "point", p = 0.66) |>
  generate(reps = 1000, type = "draw") |>
  calculate(stat = "prop")

# visualize and compute the p-value

null_dist |>
  visualize() +
  shade_p_value(obs_stat = obs_stat, direction = "greater")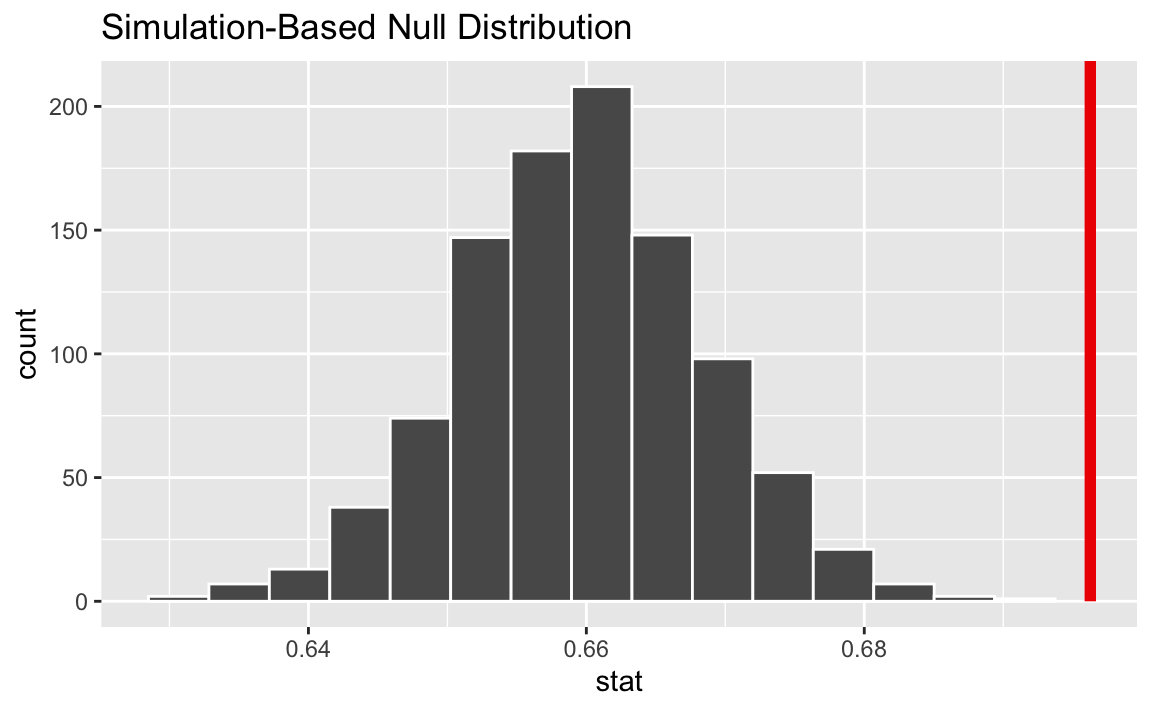

null_dist |>
  get_p_value(obs_stat, direction = "greater")

Warning: Please be cautious in reporting a p-value of 0. This result is an approximation
based on the number of `reps` chosen in the `generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.

# A tibble: 1 × 1
  p_value
    <dbl>
1       0

Our p-value is approximately zero, which is below every standard discernibility level, and therefore we reject the null. The interpretation is:

If the null were true and there were just as many certain voters in 2023 as in 2020, then there is a 0% chance we would get an estimate as or more extreme (greater) than the one we actually got. As such, the null is probably a bunch of balderdash.